문제 출처
https://school.programmers.co.kr/learn/courses/30/lessons/42892
프로그래머스
코드 중심의 개발자 채용. 스택 기반의 포지션 매칭. 프로그래머스의 개발자 맞춤형 프로필을 등록하고, 나와 기술 궁합이 잘 맞는 기업들을 매칭 받으세요.
programmers.co.kr
정답 풀이
트리를 생성하고,
트리를 탐색하면 되는 문제다.
### 0. 기존 세팅

문제에서 주어지는 `nodeinfo`를 새로운 배열로 정리 및 정렬을 해야 한다.
기준은,
- 노드의 번호는 idx+1 이 된다.
- 노드의 x값은 node[0]이 된다.
- 노드의 y값은 node[1]이 된다.
정렬은,
- y값을 기준으로 내림차순을 한다. (이유: 부모 자식 부터 차례대로 tree 생성 및 삽입 할 것임)
### 1. 트리 생성
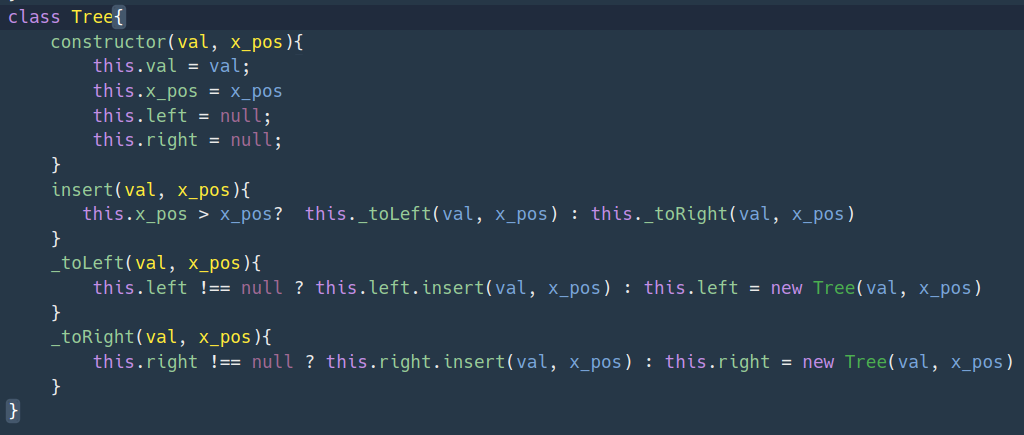
- 이진 트리를 생성할 클래스를 선언한다.
- constructor 생성자 메서드로 클래스가 인스턴스화될 때 호출된다. (초기화 작업)
- 이 생성자는 val과 x_pos라는 인자를 받아서 트리 노드의 값을 val에, x위치를 x_pos에 저장한다.
- left와 right은 null로 초기화한다.
- insert 함수는 새로운 값을 트리에 삽입하는 메서드다.
- 현재 노드의 x_pos가 새로 삽입하려는 노드의 x_pos보다 큰 경우 왼쪽 서브트리에 삽입하고, 그 반댄 오른쪽 서브트리에 삽입한다.
- _toLeft는 왼쪽 서브트리에 삽입하기 위한 헬퍼 메서드다.
- 만약 현재 노드의 왼쪽 자식이 이미 존재하면 그 자식 노드에 대해 insert 함수를 재귀적으로 호출한다.
- 만약 없다면, 새로운 tree 노드를 생성해서 현재 노드의 왼쪽 자식으로 설정한다.
- _toRight 메서드는 그 반대와 같음

- bTree를 생성하는데 rootNode를 기준으로 먼저 만든다.
- 반복문을 통해 idx =1 부터 계속 삽입한다.
### 2. 트리 탐색
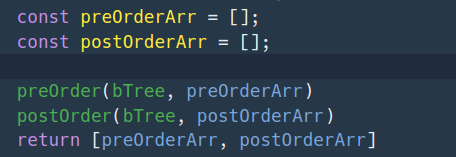
- 전위 함수에 bTree와 배열을 넣어준다 => preOrderArr에 전위 순회한 값이 담기게
- 후위 함수에 bTree와 배열을 넣어준다 => postOrderArr에 후위 순회한 값이 담기게
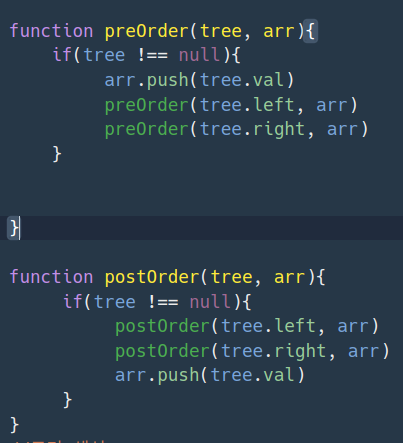
- 재귀 함수 호출인데 해당 tree가 null 값이 아닐 때까지 함수가 재귀적으로 호출된다.
- 전위 순회는 현재 노드의 값을 넣어 준 후 , 왼쪽탐색, 오른쪽 탐색
- 후위 순회는 왼쪽 탐색, 오른쪽 탐색 한 후, 현재 노드의 값을 넣어주기
정답 코드
function solution(nodeinfo) {
let preOrderArr = [];
let postOrderArr = [];
const nodes = nodeinfo.map((node, idx) =>
[idx+1, node[0], node[1]]).sort((a,b) => b[2]- a[2])
const bTree = new Tree(nodes[0][0], nodes[0][1]);
for(let i=1; i<nodes.length; i++){
bTree.insert(nodes[i][0],nodes[i][1])
}
preOrder(bTree,preOrderArr)
postOrder(bTree, postOrderArr)
return [preOrderArr, postOrderArr]
}
class Tree{
constructor(val, x_pos){
this.val = val;
this.x_pos = x_pos
this.left = null
this.right = null
}
insert(val, x_pos){
if(this.val !== null){
this.x_pos > x_pos ? this._toLeft(val, x_pos) : this._toRight(val, x_pos)
}
}
_toLeft(val, x_pos){
this.left !== null ? this.left.insert(val, x_pos) : this.left = new Tree(val, x_pos)
}
_toRight(val, x_pos){
this.right !== null ? this.right.insert(val, x_pos) : this.right = new Tree(val, x_pos)
}
}
const preOrder = (bTree, arr) => {
if(bTree !== null){
arr.push(bTree.val)
preOrder(bTree.left, arr)
preOrder(bTree.right, arr)
}
}
const postOrder = (bTree, arr) => {
if(bTree !== null){
postOrder(bTree.left, arr)
postOrder(bTree.right, arr)
arr.push(bTree.val)
}
}
++ 그외


'알고리즘 문제 풀기' 카테고리의 다른 글
| 백준 11000 : 강의실 배정 - javascript() (0) | 2024.08.24 |
|---|---|
| 백준 12015 : 가장 긴 (LIS 알고리즘, 이진탐색) - javascript (0) | 2024.08.22 |
| 백준 1744: 수 묶기 - javascript(그리디) (0) | 2024.08.21 |
| 백준 1339: 단어 수학 - javascript(그리디) (0) | 2024.08.19 |
| 백준 2110: 공유기 설치 - javascript(이진탐색, 그리디) (0) | 2024.08.19 |
