반응형
문제 출처
https://www.acmicpc.net/problem/2110
정답 풀이
흠 이 문제의 입력값을 봐보자.
집의 개수는 무려 (2<=N <=200,000) 범위이고,
공유기의 개수는 (2<= C<=N) 범위이고,
집의 좌표는 (0<=I<=1,000,000,000) 범위이다.
엄청난 범위,,, 어떤 알고리즘이 생각나는가?
이진탐색 !!!
이진탐색은 어떤 값을 기준으로 탐색해나갈 것인가가 중요하다.
여기서는 `공유기 사이의 최대거리`를 기준으로 탐색하면 되겠다.
공유기 사이가 될 수 있는 범위는
(1이상 ~ 가장 마지막 집 - 가장 첫번째 집) 이 될 것이다.
아래 그림을 보면 이해가 쉽다.
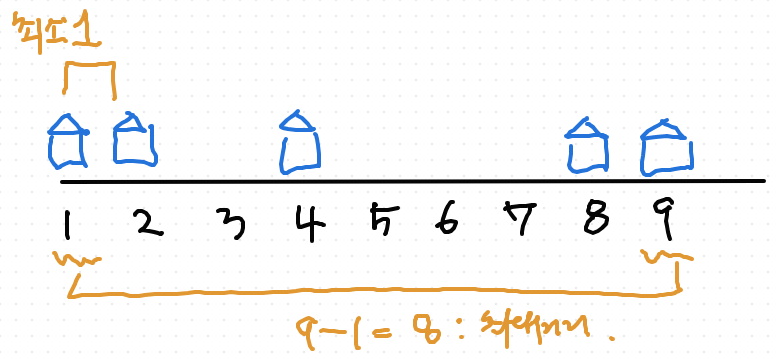
정리하자면,
- 공유기 거리의 최솟값은 : 1
- 공유기 거리의 최댓값은 : 마지막 집 위치 - 첫번째 집 위치
이제 문제를 두 부분으로 나눠서 생각하면 된다.
- 공유기 최대 거리를 이진탐색으로 찾아나간다.
- 해당 공유기 거리가 최대 거리가 되는지 확인한다. (코드에서 check 함수)
정답 코드
const input = require('fs').readFileSync('/dev/stdin').toString().trim().split('\n');
const [n,m] = input.shift().split(' ').map(v => +v)
let arr = [];
for(let i=0; i<n; i++){
arr.push(Number(input[i]))
}
arr.sort((a,b) => a-b)
function solution(n,m, arr){
let start = 1
let end = arr[n-1] - arr[0]
while(start <= end){
let mid = parseInt((start + end)/2);
if(check(mid)){
start = mid +1
}else{
end = mid - 1
}
}
return end;
function check(num){
let prev = arr[0]
let cnt = 1
for(let i=1; i<n; i++){
if(prev + num <= arr[i]){
cnt++;
prev = arr[i]
if(cnt >= m) return true
}
}
return false;
}
}
console.log(solution(n,m,arr))반응형
'알고리즘 문제 풀기' 카테고리의 다른 글
| 백준 1744: 수 묶기 - javascript(그리디) (0) | 2024.08.21 |
|---|---|
| 백준 1339: 단어 수학 - javascript(그리디) (0) | 2024.08.19 |
| 프로그래머스: 자물쇠와 열쇠 - javascript(단순 구현) (0) | 2024.08.18 |
| 프로그래머스: [3차] 자동완성 - javascript(체이닝, 트리) (0) | 2024.08.10 |
| 프로그래머스: 무지의 먹방 라이브 - javascript(반복문 구현) (2) | 2024.08.06 |
