문제 출처
https://school.programmers.co.kr/learn/courses/30/lessons/118668
프로그래머스
코드 중심의 개발자 채용. 스택 기반의 포지션 매칭. 프로그래머스의 개발자 맞춤형 프로필을 등록하고, 나와 기술 궁합이 잘 맞는 기업들을 매칭 받으세요.
programmers.co.kr
문제 풀이 힌트
DP를 활용하는 문제이다.
DP 배열
- dp[i][j] : (알고력 i, 코딩력 j) 상태에 도달하는 데 필요한 최단 시간
DP 배열 업데이트
- 알고리즘을 공부하여 알고력을 1 높이는 경우:
dp[i+1][j] = min(dp[i+1][j], dp[i][j]+1) - 코딩을 공부하여 코딩력을 1 높이는 경우:
dp[i][j+1] = min(dp[i][j+1], dp[i][j]+1) - 문제 하나를 선택하여 알고력과 코딩력을 높이는 경우:
dp[i+alp_rwd][j+cop_rwd] = min(dp[i+alp_rwd][j+cop_rwd], dp[i][j]+cost) (단, i >= alp_req이고 j >= cop_req)
이 문제는 DP를 어떻게 생각해내고,
어떻게 구현할지도 중요하지만,
DP 배열 안에서 탐색할 때, 그 값이 배열 이외의 값에 접근하지 않도록
조건을 걸어주는 것이 중요하다.
주의할 점 )
모든 문제를 다 풀기 위한 알고력과 코딩력은 어떻게 구할까?
problems를 반복문으로 접근하면서 각각 최댓값을 찾으면 될 것이다.
어처피 변경될 값이니, 초기값을 0으로 설정해도 될까?
=> 절대 안된다.
초기값은 alp, cop로 설정해야 한다.
왤까?
우리의 dp 그래프는 주어진 alp, cop을 기점으로 화살표 쪽으로 최소값을 채워나갈 것인데,
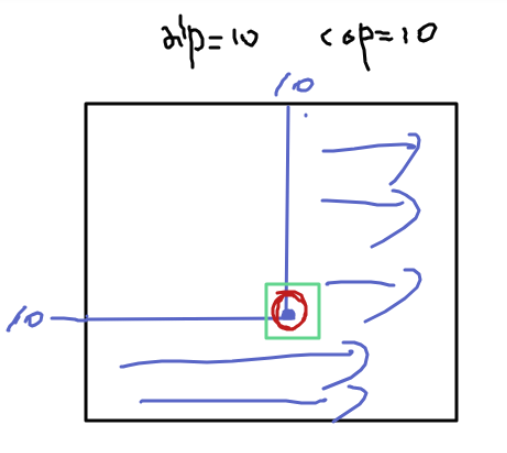
만약 problems의 최대 알고력 = 3 과 최대 코딩력 = 4 가 필요하면 어떻게 되나?
=> 이미 기존의 알고력과 코딩력으로 모든 문제를 풀 수 있으니 , 답은 0 이 될 것이다.
정리하자면, 우리의 기존 알고력과 코딩력보다 더 많은 알고력 혹은 더 많은 코딩력이 필요한 경우만 그래프를 그려서 빈 값을 채워나가는 것이다. 마지막에 dp[maxAlp][maxCop] 이 값이 답이 된다.
그러니, 기존 알고력과 코딩력으로 문제를 모두 풀 수 있는 경우에는,
maxCop의 값이 = cop이고,
maxAlp의 값이 = alp이다.
dp[maxAlp][maxCop]는 값이 0으로 채워져있다.
그러니 그 경우엔 모든 답이 0 이 될 것이다.

정답 풀이 코드
function solution(alp, cop, problems) {
let maxAlp = alp;
let maxCop = cop;
problems.forEach((pro) => {
maxAlp = Math.max(maxAlp, pro[0]);
maxCop = Math.max(maxCop, pro[1]);
});
let dp = Array.from({length: maxAlp + 1}, () => new Array(maxCop + 1).fill(Infinity));
dp[alp][cop] = 0;
for(let i = alp; i <= maxAlp; i++) {
for(let j = cop; j <= maxCop; j++) {
if(i === maxAlp && j === maxCop) break;
if (i + 1 <= maxAlp) dp[i + 1][j] = Math.min(dp[i + 1][j], dp[i][j] + 1);
if (j + 1 <= maxCop) dp[i][j + 1] = Math.min(dp[i][j + 1], dp[i][j] + 1);
problems.forEach((pro) => {
const [alpReq, copReq, alpRwd, copRwd, cost] = pro;
if (i >= alpReq && j >= copReq) {
let newAlp = Math.min(maxAlp, i + alpRwd); //i의 새로운 좌표가 dp 배열을 넘어가면 안됨
let newCop = Math.min(maxCop, j + copRwd); //j의 새로운 좌표가 dp 배열을 넘어가면 안됨
dp[newAlp][newCop] = Math.min(dp[newAlp][newCop], dp[i][j] + cost); // 기존의 값보다 작으면 업데이트
}
});
}
}
return dp[maxAlp][maxCop];
}Only 풀이 코드
function solution(alp, cop, problems) {
let maxAlp = alp;
let maxCop = cop;
problems.forEach((pro) => {
maxAlp = Math.max(maxAlp, pro[0]);
maxCop = Math.max(maxCop, pro[1]);
});
let dp = Array.from({length: maxAlp + 1}, () => new Array(maxCop + 1).fill(Infinity));
dp[alp][cop] = 0;
for(let i = alp; i <= maxAlp; i++) {
for(let j = cop; j <= maxCop; j++) {
if(i === maxAlp && j === maxCop) break;
if (i + 1 <= maxAlp) dp[i + 1][j] = Math.min(dp[i + 1][j], dp[i][j] + 1);
if (j + 1 <= maxCop) dp[i][j + 1] = Math.min(dp[i][j + 1], dp[i][j] + 1);
problems.forEach((pro) => {
const [alpReq, copReq, alpRwd, copRwd, cost] = pro;
if (i >= alpReq && j >= copReq) {
let newAlp = Math.min(maxAlp, i + alpRwd);
let newCop = Math.min(maxCop, j + copRwd);
dp[newAlp][newCop] = Math.min(dp[newAlp][newCop], dp[i][j] + cost);
}
});
}
}
return dp[maxAlp][maxCop];
}
'알고리즘 문제 풀기' 카테고리의 다른 글
| 프로그래머스: 산 모양 타일링 - javascript(dp) (0) | 2024.07.15 |
|---|---|
| 프로그래머스: [1차] 추석 트래픽- javascript(시간함수, 구간 최대값) (0) | 2024.07.14 |
| 프로그래머스: 표 병합 - javascript(Union-Find) (0) | 2024.07.11 |
| 프로그래머스 : 블록 이동하기 - javascript (bfs) (0) | 2024.07.01 |
| MinHeap 정렬 - javascript (0) | 2024.06.25 |
